هوش مصنوعی با نرم افزار کنترل تردد خودرو (6)
10 اردیبهشت 1402اصلاح تصویر و حذف نویز در متلب 2 (20)
3 آبان 1402
اصلاح تصویر و حذف نویز در متلب 3
روش آماری فیلتر NSPR در نرم افزار متلب
بخش 21 آموزش برنامه نویسی درنرم افزار متلب
در این بخش میخوانیم :
1- روش آماری فیلتر NSPR
2- تخمین زدن با روش آماری واریانس
3- تابع deconvwnr
4- فراخوانی تابع deconvwnr به روش J = deconvwnr ( I , PSF , NSR )
5- فرا خوانی تابع deconvwnr به روش J = deconvwnr ( I , PSF , NCORR , ICORR )
در روش آماری فیلتر NSPR در متلب زمانی که خط بالای NSPR را برمیداریم یعنی NSPR ثابت است .
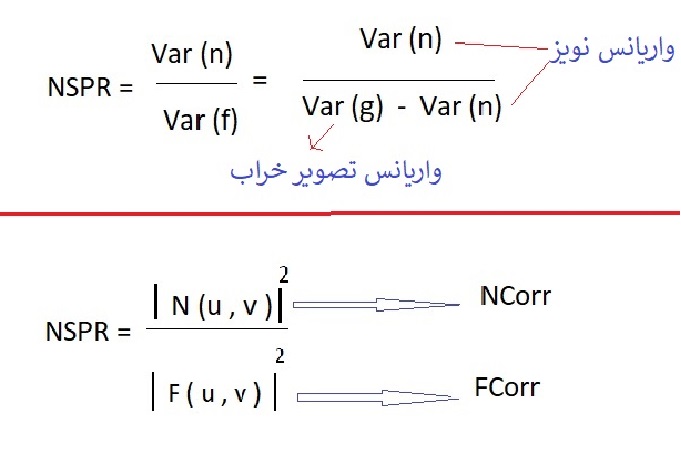
این روش همان مفهوم قبل را دارد اما از دید آماری NSPR را توصیف میکند .
PSF برای تبدیل مکانی استفاده میشود که همان ماتریس وزنی است .
NSR یک پارامتر است که اندازه نویز به سیگنال را نشان میدهد .
NCORR ارتباط نویز با خودش .
ICORR ارتباط تصویر با خودش .
حذف نویز را در این پارامتر بررسی میکنیم .
-
Clc ;
Clear ;
Close all ;
% % Read Image
f =imread ( ‘ Cameraman . tif ‘ ) ;
f = im2double (f) ;
% % Apply Motion Filter
MotionLength = 7 ;
MotionAngle = 45 ;
PSF = fspecial ( ‘ motion ‘ , MotionLength , MotionAngle ) ;
g1 = imfilter ( f , PSF) ;
% % Add Noise
NoiseMean = 0 ;
NoiseVar = 0 . 01 ;
g2 = imnoise ( g1 , ‘gaussian ‘ , NoiseMean , NoiseVar ) ;
% % Wiener Deconvolution
% % Results
figure ;
subplot ( 2 , 2 , 1 ) ;
imshow ( f ) ;
title ( ‘ Original Image ‘ ) ;
subplot ( 2 , 2 , 2 ) ;
imshow ( g1) ;
title ( ‘ Blurred Image ‘ ) ;
subplot ( 2 , 2 , 3) ;
imshow ( g2) ;
title ( ‘ Blurred and Noisey Image ‘ ) ;

بازیابی تصویری با 45 درجه چرخش از دستور J = deconvwnr ( I , PSF , NSR ) که باید نویز آن را هم از بین ببریم .
در این دستور فرض ما بر این است که PSF را داریم .
با استفاده از روش آماری واریانس مورد سنجش قرار میدهیم .
-
% % Wiener Deconvolution
% ImageVar = Var (f(:)) ;
% NSPR = NoiseVar ;
Fhat 1 = deconvwnr (g2 , PSF , 0 ) ;
% % Results
figure ;
subplot ( 2 , 3 , 1 ) ;
imshow ( f ) ;
title ( ‘ Original Image ‘ ) ;
subplot ( 2 , 3 , 2 ) ;
imshow ( g1) ;
title ( ‘ Blurred Image ‘ ) ;
subplot ( 2 , 3 , 3) ;
imshow ( g2) ;
title ( ‘ Blurred and Noisey Image ‘ ) ;
subplot ( 2 , 3 , 4) ;
imshow ( fhat1 ) ;
title ( ‘ Recovered Image ( NPSR = 0 ) ‘ ) ;

اگر هیچ نویزی وجود نداشته باشد چنین تصویر مخدوشی به ما میدهد که برای ما کارایی ندارد .
از تحلیل آماری NSPR برای یافتن تصویر اصلی کمک میگیریم .
-
% % Add Noise
NoiseMean = 0 ;
NoiseVar = 0 . 001 ;
g2 = imnoise ( g1 , ‘gaussian ‘ , NoiseMean , NoiseVar ) ;
% % Wiener Deconvolution
NSPR1 = 0 ;
Fhat 1 = deconvwnr (g2 , PSF , NSPR1 ) ;
ImageVar = Var (f (:) ) ;
NSPR2 = NoiseVar / ImageVar ;
Fhat2 = deconvwnr (g2 , PSF , NSPR2 ) ;
% % Results
figure ;
subplot ( 2 , 3 , 1 ) ;
imshow ( f ) ;
title ( ‘ Original Image ‘ ) ;
subplot ( 2 , 3 , 2 ) ;
imshow ( g1) ;
title ( ‘ Blurred Image ‘ ) ;
subplot ( 2 , 3 , 3) ;
imshow ( g2) ;
title ( ‘ Blurred and Noisey Image ‘ ) ;
subplot ( 2 , 3 , 4) ;
imshow ( fhat1 ) ;
title ( ‘ Recovered Image ( NPSR = 0 ) ‘ ) ;
subplot ( 2 , 3 , 5) ;
imshow ( fhat2 ) ;
title ( [ ‘ Recovered Image ( NPSR = ‘ num2str ( NSPR2) ‘ ) ‘ ] ) ;

با کمتر کردن ده برابری واریانس نویز توانستیم اثر حرکت 45 درجه ای را از بین ببریم و از لحاظ وضوح به تصویر اصلی نزدیکتر شدیم حالا با استفاده از روش دیگری اثر نویز را بهبود میبخشیم .
-
% % Wiener Deconvolution
NSPR1 = 0 ;
Fhat 1 = deconvwnr (g2 , PSF , NSPR1 ) ;
ImageVar = Var (f (:) ) ;
NSPR2 = NoiseVar / ImageVar ;
Fhat2 = deconvwnr (g2 , PSF , NSPR2 ) ;
NSPR3 = 0 .05 ;
Fhat3 = deconvwnr (g2 , PSF , NSPR3 ) ;
% % Results
figure ;
subplot ( 2 , 3 , 1 ) ;
imshow ( f ) ;
title ( ‘ Original Image ‘ ) ;
subplot ( 2 , 3 , 2 ) ;
imshow ( g1) ;
title ( ‘ Blurred Image ‘ ) ;
subplot ( 2 , 3 , 3) ;
imshow ( g2) ;
title ( ‘ Blurred and Noisey Image ‘ ) ;
subplot ( 2 , 3 , 4) ;
imshow ( fhat1 ) ;
title ( ‘ Recovered Image ( NPSR = 0 ) ‘ ) ;
subplot ( 2 , 3 , 5) ;
imshow ( fhat2 ) ;
title ( [ ‘ Recovered Image ( NPSR = ‘ num2str ( NSPR2) ‘ ) ‘ ] ) ;
subplot ( 2 , 3 , 6) ;
imshow ( fhat3 ) ;
title ( [ ‘ Recovered Image ( NPSR = ‘ num2str ( NSPR3) ‘ ) ‘ ] ) ;

در این حالت حذف نویز بیشتری انجام شده ولی نسبت به تصویر قبلی بیشتر تار شده ولی نسبت به تصاویر اولیه بالای صفحه وضوح و شفافیت بیشتری دارد .
حالا روش دیگر فرا خوانی با تابع J = deconvwnr ( I , PSF , NCORR , ICORR ) را اعمال میکنیم .
ابتدا باید طیف نویز را محاسبه و پیدا کنیم .
-
SN = abs (fft2 (g2 – g1)) . ^2 ;
NCORR = fftshift (real (ifft2 (SN)) ;
SF = abs (fft2(f)) . ^2 ;
FCORR = fftshift (real (ifft2 (SF))) ;
NSPR = NCORR . / FCORR ;
Fhat3 = deconvwnr ( g2 , PSF , NCORR , FCORR ) ;

همبستگی سیگنال یک عدد ثابت نیست و نسبت به نقاط مختلف تصویر عوض میشود به این حالت میگن کُریلیشن با خودش است .
تصویر خیلی واضحتر از قبل شده فقط کمی نویز خطوط افقی عمودی روی اطراف تصویر زیاد شده که برای از بین بردن آنها از تابع J = edgetaper (I , PSF) استفاده میشود
-
PSF2 = fspecial (‘gaussian ‘ , 60 , 10 ) ;
Fhat4 = edgetaper (fhat3 , PSF2 ) ;

نویز حواشی تصویر را کم کرد وشباهت این تصویر نسبت به تصویر اصلی از بقیه توابعی که امتحان کردیم بیشتر است .
با اعمال هر فیلتر نتایج متنوعی را یافتیم .










