- شرکت اندیشه تراشه ویرا
- دفتر تهران: 02176490358-09120613870
- دفتر مشهد: 05138554285-09155177027
- info@Tarashe.Net

اصلاح تصویر و حذف نویز در متلب 2 (20)
3 آبان 1402تشخیص پلاک تار از فیلم دوربین مداربسته آموزش: راهنمای کامل و کاربردی
12 مهر 1404اصلاح تصویر و حذف نویز در متلب
بخش 19 آموزش برنامه نویسی درنرم افزار متلب
در این بخش میخوانیم :
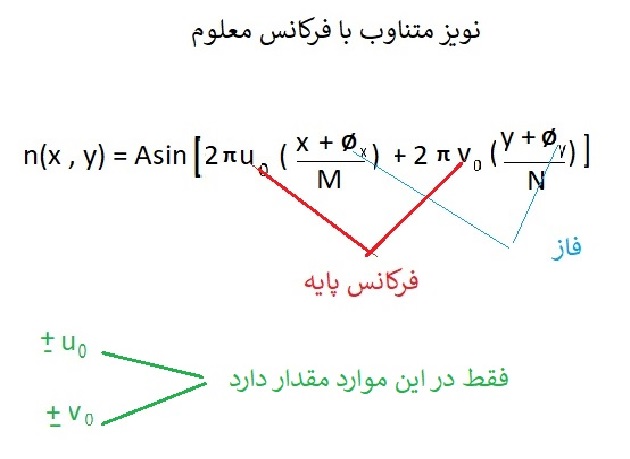
1- نویز متناوب با فرکانس معلوم
2- فرمول پایه اصلاح تصویر
3- آشنایی با کار کرد فیلترهای مکانی
4- آماده سازی فیلترها
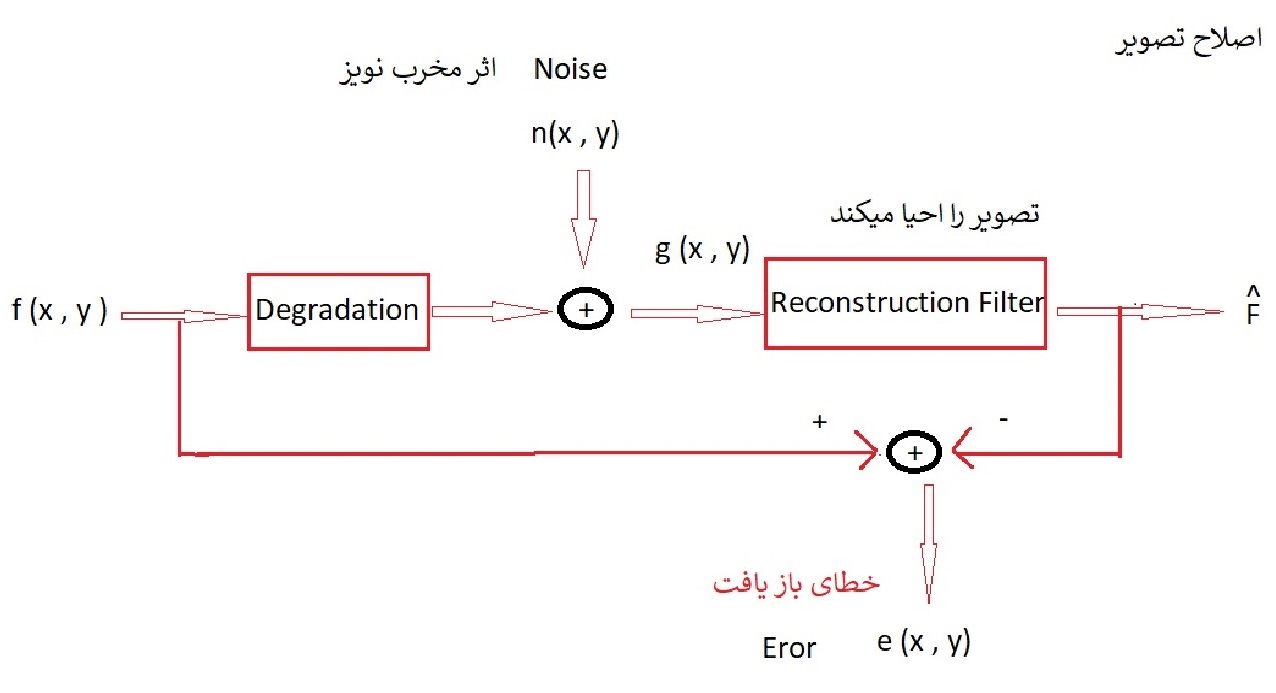
اصلاح تصویر و حذف نویز و بازیافت تصویر از کاربرد های پردازش تصویر میباشد .
فرمول پایه همه روش های اصلاح تصویر :
هدف از طی مراحل اصلاح تصویر یافتن روش هایی برای رسیدن از g به f^ است که تقریب تصویر اصلی میباشد .
(f^ را اِف هَد میخوانیم )
در اصلاح تصویر و حذف نویز متلب N , H در فرمول مجهول است و یافتن عین خطا ممکن نیست مگر بدانیم چه مدل نویز یا خطایی رخ داده ، از ساده ترین حالت ها نویز متناوب با فرکانس معلوم میباشد .
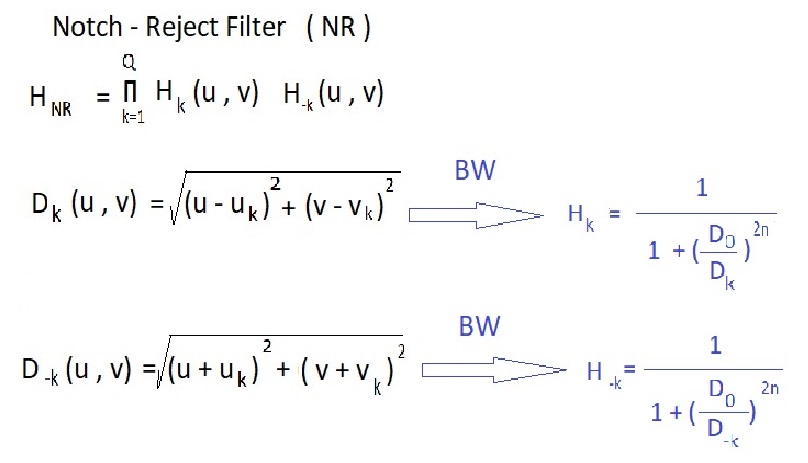
تابع دلتای دیراک که برچهار ترکیب ( u , – u , -v , +v + ) تمرکز دارد .
هنگامی که u به uk نزدیک باشد حاصل صفر است و هنگامی که در بی نهایت باشد حاصل یک است هر چه به فرکانس uk نزدیک شود حذف است .
انواع فیلتر های مکانی حذف نویز در متلب :
1- فیلتر مکانی Average یا میانگین که با تابع fspecial در متلب نمایش و با average اجرا میشود .
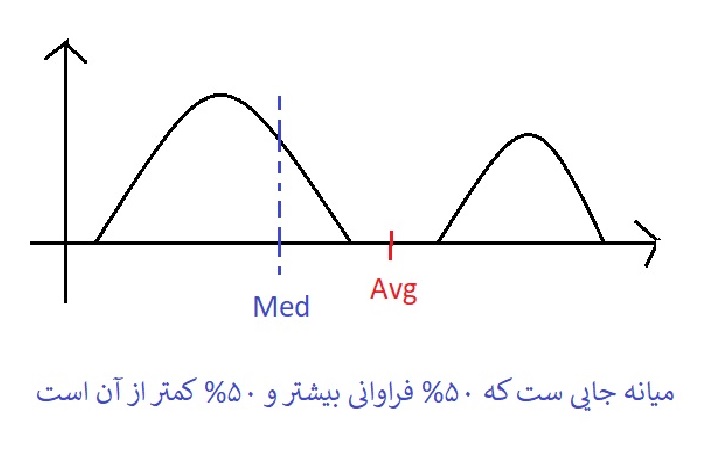
2- فیلتر مکانی Median یا میانه که با تابع medfilt2 در متلب اجرا میشود داده ای که نمایش میدهد همیشه میان داده های ورودی است .
3- فیلتر مکانی میانگین هندسی که با تابع colfilt در متلب اجرا میشود .
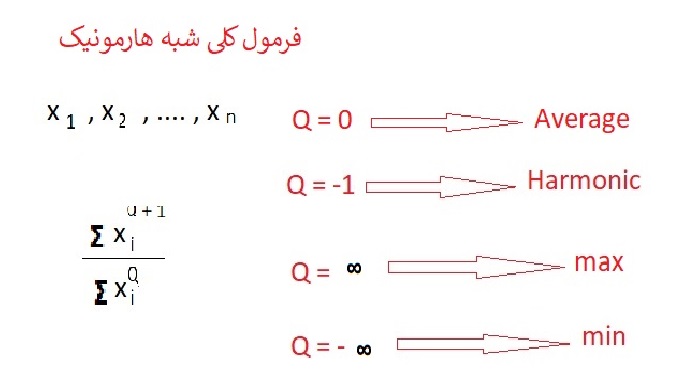
4- فیلتر مکانی هارمونیک یا میانگین توافقی که با تابع colfilt در متلب اجرا میشود .
5- فیلتر مکانی Contra harmonic یا شبه هارمونیک که با تابع colfilt در متلب اجرا میشود .
6- فیلتر مکانی Max یا بیشینه که با تابع ordfilt2 در متلب اجرا میشود .
7- فیلتر مکانی Min یا کمینه که با تابع ordfilt2 در متلب اجرا میشود .
8- فیلتر مکانی mid-point یا نقطه میانی که با تابع colfilt در متلب اجرا میشود .
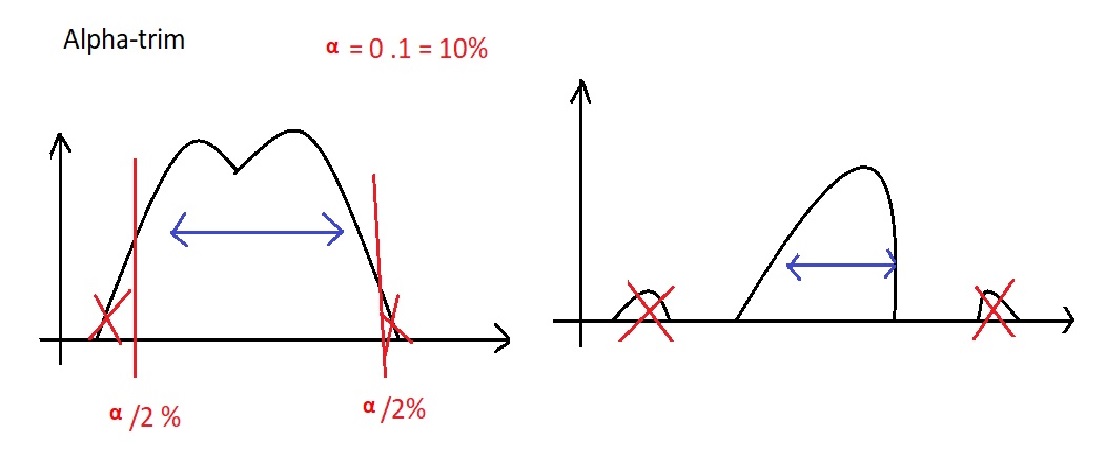
9- فیلتر مکانی Alpha – trim که به طریق حذف کردن یا بریدن از ابتدا یا انتها کار میکند .
با اعمال هر کدام از این فیلتر ها به روی تصویر میتوانیم نویزهایی را از تصویر کم کنیم .
از فیلترهای مکانی در نرم افزار پارکینگ و اتوماسیون پارکینگ استفاده میگردد.
اجرای فیلترها :
-
function g = spatialFilter ( Type , Size , Varargin ) if nargin < 3 I I isempty ( size ) size = [3 3] ; end if nume 1 (size ) = = 1 size = [size size] ; end Type = Lower ( Type ) ; Switch Type Case ‘ median ‘ g = medfilt2 ( f , size ) ; Case { ‘ average ‘ , ‘ mean ‘ } W = fspecial ( ‘average ‘ , size ) ; G = imfilter ( f , w ) ; Case { ‘ geomtric ‘ , ‘gmean’ , ‘geomean’ , ‘ geomtricmean ‘} g = colfilt (f , size , ‘ sliding ‘ , @GeomtricMean ) ; Case { ‘ harmonic ‘ , ‘ hmean ‘ , ‘ harmean ‘ , ‘ harmonicmean ‘} g = colfilt (f , size , ‘ sliding ‘ , @ HarmonicMean) ; Case { ‘ charmonic ‘ , ‘ contraharmonic ‘} if isempty ( Varargin ) Q = 1 ; else Q = Varargin } 1 { ; end fun = @ (X) ContraHarmonicMean ( X , Q ) ; g = colfilt (f , size , ‘ sliding ‘ , fun ) ; Case ‘ max ‘ g= ordfilt2 (f , prod ( size) , true ( size ) ) ; Case ‘ min ‘ g= ordfilt2 ( f , 1 , true ( size ) ) ; Case ‘ midpoint ‘ gmin = ordfilt2 ( f , 1 , true ( size ) ) ; gmax= ordfilt2 (f , prod ( size) , true ( size ) ) ; g=( gmin + gmax ) /2 ; Case ‘ alphatrim ‘ if isempty ( Varargin ) alpha = 0 . 1 ; else alpha = Varargin } 1 { ; end fun = @ ( X ) AlphaTrimMean ( x , alpha ) ; g = colfilt ( f , size , ‘ sliding ‘ , fun ) ; Other wise Error ( ‘ Undefined filter type . ‘ ) ; end function gm= GeomtricMean (X) gm= exp (mean (Log ( X ) ) ) ; end function hm = HarmonicMean (X) hm= 1./mean (1./X) ; end function chm= ContraHarmonicMean (X) Chm= Sum ( X . ^ (Q+1) ) ./Sum( X . ^ Q ) ; end function atm = AlphaTrimMean ( X , alpha ) atm = zeros ( 1 , size ( x , 2 ) ) ; for j = 1 : nume 1 (atm ) xtj = AlphaTrim ( x ( : , j ) , alpha ) ; atm ( j ) = mean ( xtj ) ; end function xt= AlphaTrim ( X , alpha ) nx = numel ( X ) ; nt = 2*round ( alpha * nx/2 ) ; xt = sort ( X ) ; xt ( [ 1 : nt/2 end – nt/2 + 1 : end ] ) = [ ] ; end