spatial filtering روش های فیلترینگ مکانی در نرم افزار متلب (8)

spatial filtering روش های فیلترینگ مکانی در نرم افزار متلب

 

بخش 8 آموزش برنامه نویسی درنرم افزار متلب 

در این بخش میخوانیم :

1- آشنائی با مراحل  spatial filtering در نرم افزار متلب

2- نمونه مثال برای ماتریس [3 و 3]

3- کار با اپراتور correlation

4- کار با تابع imfilter

5- آشنائی با اصطلاحات symmetric  ,  replicate  ,  circular

6- چگونگی دوران ماتریس

یکی دیگر از روش های نمایش دادن تصویر در حوزه مکان فیلترینگ مکانی ، یا فضائی یا spatial filtering است که در نرم افزار متلب به کاربردهای این بخش در پردازش تصویر میپردازیم .

1- نقطه ای از تصویر را با مختصات (x, y ) در نظر میگیریم . در ریاضی هر نقطه ای میتواند باشد اما در متلب از یک و یک شروع میشود تا آخر .

2- عملیات مربوط به فیلتر مکانی را روی (x, y ) شروع میکنیم .

3- نتیجه مرحله قبل را به عنوان جواب فیلتر در نقطه (x, y ) قرار میدهیم و در تصویر پاسخ عددی را که از مرحله قبل به دست اوردیم در نقطه (x, y ) میگذاریم .

4- سراغ نقطه بعد میرویم و مراحل را دوباره روی آن تکرار میکنیم  کار را ادامه میدهیم تا همه نقاط تصویر یک به یک روند فیلتر مکانی روی آن اجرا شود .

 این چهار مرحله ئ یک فیلتر مکانی یا فضایی است .

مثلا :

در تصویر M . N نقطه ی (x, y ) به مبدا مختصات (1 و 1) این نقطه هشت تا همسایه دارد متناظر با این نقطه یک عملیات خطی در نظر میگیریم الان دو ماتریس [3  3] داریم باید این عملیات را روی تک تک نقاط تصویر انجام دهیم .

 

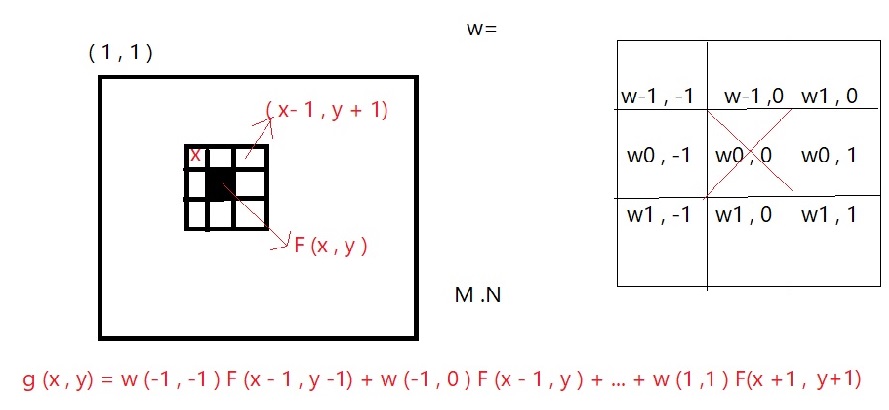
هر یک با عضو متناظرش ضرب میشود .

 فرمول بسته ریاضی آن میشود:

یک به یک هر (x, y )  آن را حساب میکنیم ، یک فیلتر خطی مکانی است به این کار Linear Spatial Filter میگویند ، حالت کلی آن یک ماتریس با ابعاد فرد میباشد که یکی از اپراتورهای پایه میباشد  .

 

 

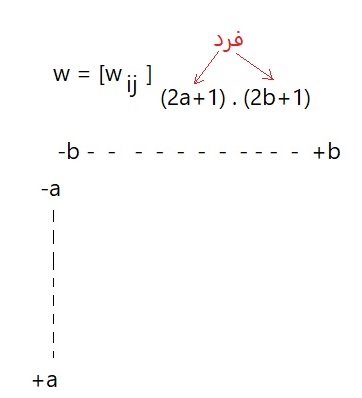
باز شده این فرمول به شکل کلی :

 

 

اپراتور  correlation قرینه اپراتور convolution در ریاضی است ، گویا w را 180 درجه چرخاندیم .

در روش های spatial filtering یکی از توابع متلب تابع  im filter میباشد که یک فیلتر خطی است .

تابع im filter  تابع correlation را اجرا میکند .

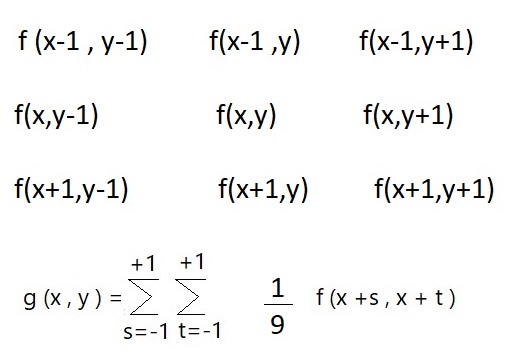
یک ماتریس [3  3] که هر نقطه آن میانگین 9 نقطه که حول یک نقطه خاص هستند میباشد .

عمل میانگین همه را به یک سمت میبرد و نویز زیاد تصویر را از بین میبرد و تصویر را مات (اصطلاحا اسموس) میکند .

 

1. Clc ;
   Clear ;
   Close all ;
   Img 1 = imread ( ‘ rice . png ‘ ) ;
   A = 1 ;
   W = ones ( 2 * a + 1 ) ;
   W = w / sum (w ( : ) ) ;
   img 2 = imfilter ( img 1 , w ) ;
   figure ;
   subplot ( 1 , 2 , 1 ) ;
   imshow ( img 1 ) ;
   title ( ‘original Image ‘ ) ;
   subplot ( 1 , 2 , 2 ) ;
   imshow (img 2 ) ;
   title (‘ After Average Filter ‘ ) ;
   
   
   

کمی تصویر مات شده .

 تصویر مات تر میشود اگر اندازه a بیشتر شود .

برای نقاط حاشیه تصویر چه طور رفتار میکنیم؟

 

پیدا کردن حاشیه در ساخت و تولید نرم افزار پلاک خوان برای هوشمند سازی و نیز تشخیص چهره مورد استفاده قرار میگیرد ، در این باره میتوانید روش کارکرد دستگاه پارکینگ هوشمند و نیز راهبند هوشمند پارکینگ را ملاحظه نمایید.

یکی از استفاده های از پردازش تصویر در نرم افزار پلاک خوان و نیز اتوماسیون پارکینگ و سیستم نرم افزار کنترل تردد خودرو میباشد. نرم افزار کنترل تردد خودرو بصورت هوشمند پلاکهای خودرو های عبوری را شناسایی مینماید.

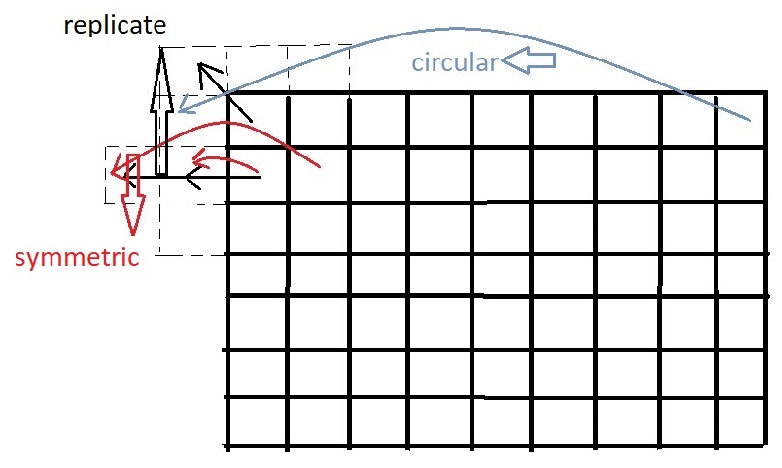
برای حاشیه تصویر از چند روش میتوانیم استفاده کنیم :

در روش circular از تکرار آخرین نقطه سطر یا ستون استفاده میشود ، در روش  symmetric به شکل متقارن عمل میشود ، در روش replicate با نقاط ثابت تکرار میشود.

علاوه بر روش های بالا که برای تکثیر استفاده میشوند ، میتوان با قرار دادن یک عدد ثابت این کار را انجام داد .

 

اطراف تصویر تار یک حاله سیاه رنگ به وجود آمده .

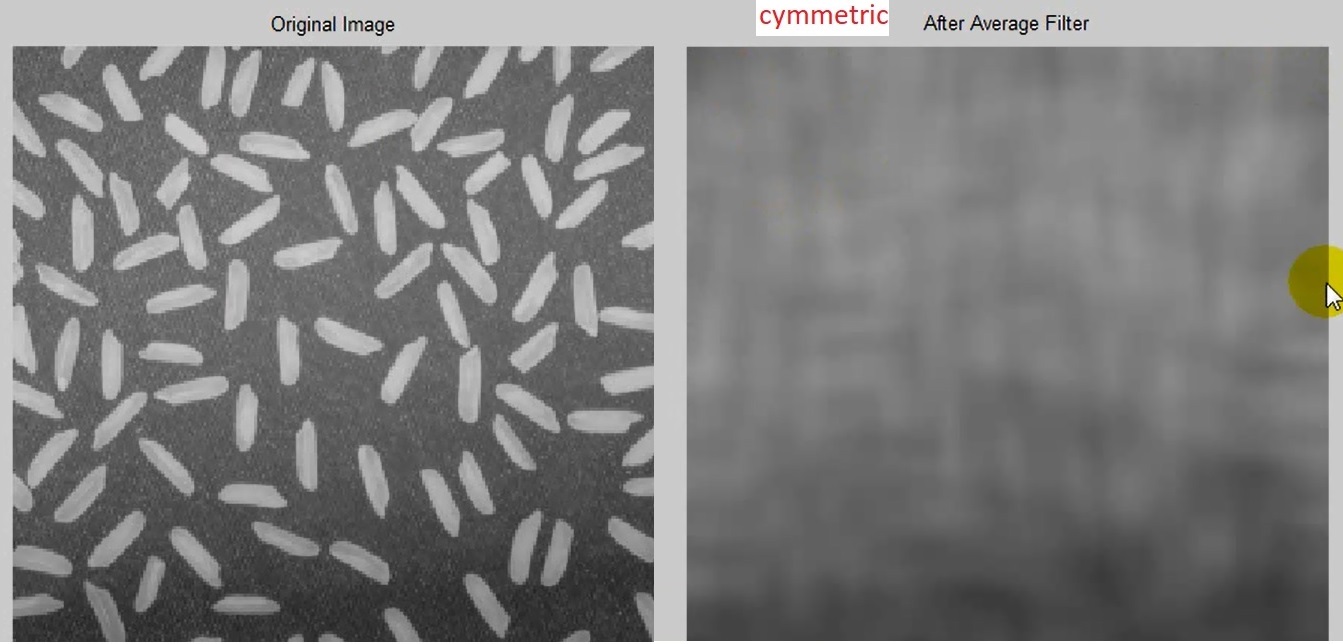
با استفاده از روش symmetric سیاهی اطراف از بین رفت .

زمانی که باید به اول یا آخر تصویر چیزی اضافه شود از تابع Output Size Options که دو حالت دارد میرویم :

same یعنی به اندازه همان تصویر ورودی نمایش داده شود ، full یعنی چیزهای اضافه شده را هم نمایش بدهد .

1. Img 1 = imread (‘ rice . png ‘ ) ;
   A= 15 ;
   W= ones ( 2* a + 1 ) ;
   W=w / sum ( w ( : ) ) ;
   Img 2 = imfilter ( img , w , ‘ circular ‘ , ‘ full ‘ ) ;
   Figure ;
   Subplot ( 1 , 2 , 1) ;
   Imshow ( img 1 ) ;
   Title ( ‘Original Image ‘ ) ;
   Subplot ( 1 , 2 , 2 ) ;
   Imshow ( img 2 ) ;
   Title ( ‘ After Average Filter ‘ ) ;

 

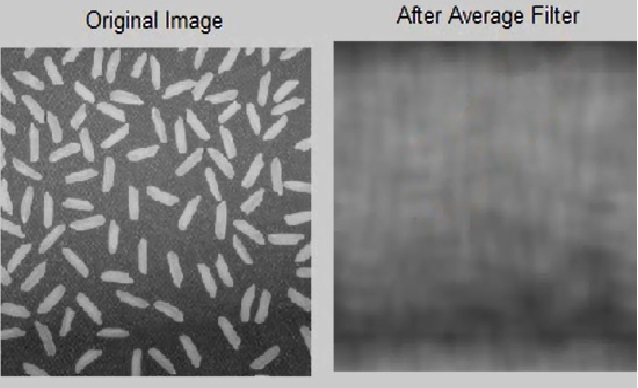
  به دو روش corr و conv میتوانیم ماتریس را ترکیب کنیم .

   این دو دستور با هم معادل هستند اگر ماتریس را دوران دهیم .

 

برای تغییر جهت یک عملگر باید آن را دوران دهیم .

کارکرد افقی بعضی عملگرها را میتوانیم با یک دوران عمودی کنیم .

 

 ادامه آموزش متلب در بخش 9