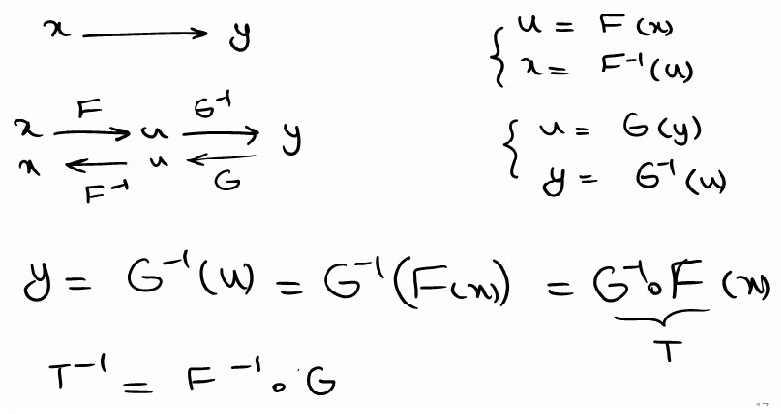هیستوگرام هدف و شدت نور تصاویر در متلب (7)

هیستوگرام هدف و شدت نور تصاویر در متلب 

بخش 7 آموزش برنامه نویسی درنرم افزار متلب 

در این بخش میخوانیم :

1- تابع CDF 

2- تابع PDF

3- هیستوگرام هدف

4- تابع Hgram

5- تابع  adapthisteq

 

بررسی توزیع ساده تر.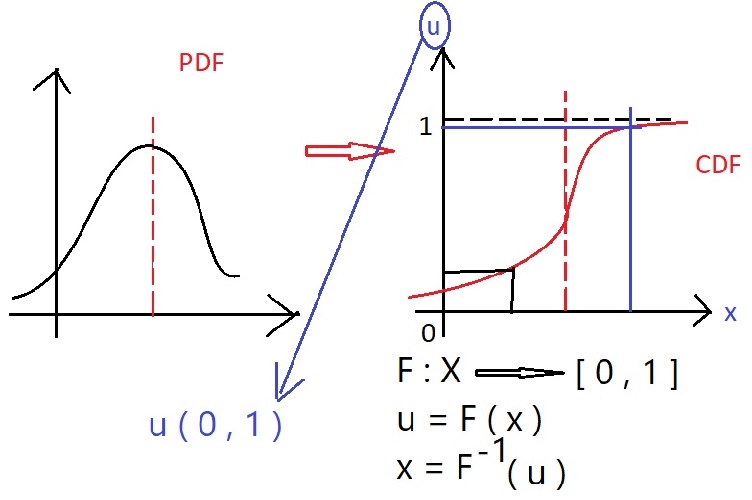

 

تابع تجمعی احتمال که علامت اختصاری آنCDF است ، شرط یک به یک بودن یک تابع صعودی بودن آن است که لازم است مشتق آن همیشه مثبت حتی صفر هم نباید باشد .از کارکردهای آن تناظر یک به یک بین مقدارهای تصادفی در هرتوزیع آماری پیوسته است .

CDF یک تابع صعودی است اگر مقدار PDF بزرگتر از صفر باشد ( PDF مشتق CDF است)

در هیستوگرام  U به طور یکنواخت از همه طیف های رنگی استفاده شده اگر آن را ترسیم کنیم یک خط صاف میشود که بهترین هیستوگرام از یک تصویر است .

نگاشت غیر خطی هر تصویر را یکنواخت سازی هیستوگرام گویند به طوری که در هر تصویر CDF  معادل با هر روشنائی u

را محاسبه کنیم u ها را یک به یک به جای x  ها قرار دهیم .

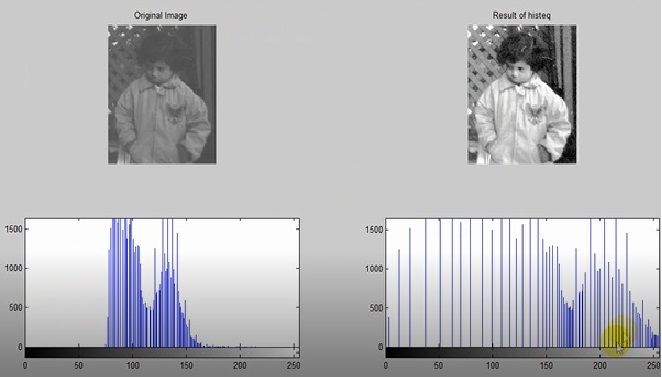
 در هیستوگرام کوالیزیشن نتیجه تصاویر چه میشود ؟

 

1. Histeq
   Syntax
   J = histeq ( I , hgram )
   J = histeq ( I , n )
   [ J , T ] = histeq ( I  , … )
   Newmap = histeq ( X , map , hgram )
   Newmap = histeq ( X , map )
   [ newmap , T ] = histeq ( X , … )
   Img 4 = histeq ( img 1 )

2. 

 

نزدیک بودن لِوِلها از لحاظ یکنواختی بهتر است .

برای این که بهینه سازی را سریع اجرا کند هیستوگرام را به هیستوگرام نزدیک به خط تبدیل میکند .

از هیستوگرام در پردازش تصویر یافتن قاب پلاک در نرم افزار پلاک خوان یا نرم افزار کنترل تردد خودرو استفاده میشود. نرم افزار پلاک خوان در دستگاه پارکینگ هوشمند مورد استفاده قرار میگیرد، برای استفاده از نرم افزار پلاک خوان در دستگاه پارکینگ و کنترل تردد خودرو هوشمند از یک dll واسط برای برقراری ارتباط جهت تبدیل متن پلاک از نرم افزار پلاک خوان به نرم افزار پارکینگ یا اتوماسیون پارکینگ داخل دستگاه پارکینگ استفاده میگردد.

تفاضل بینCDF توزیع یکنواخت و تابع تولید را به حداقل میرساند در تصاویر پیوسته حتما فِلَت میشود برای تصاویرگسسته این امکان نیست .

در هیستوگرام مچینگ (Histogram Matching) اختلاف آن را با هیستوگرام مبدا در نظر میگیرد .

 

1. I = imread ( ‘tire . tif ‘ ) ;
   J = histeq ( I ) ;
   Imshow ( I );
   Figure , imshow ( J )

 

 

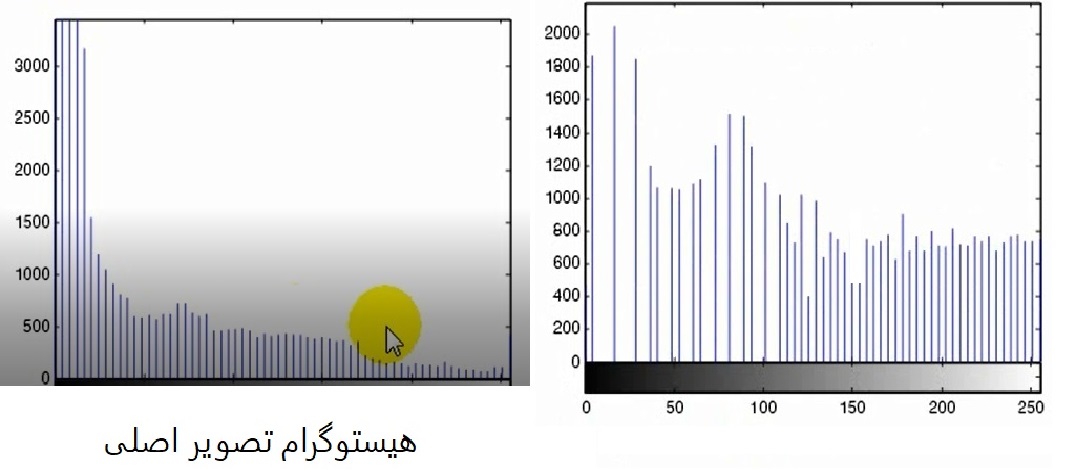
هیستوگرام کوالایز اختلاف فلت و تصویر اصلی را به حداقل میرساند .

کار دیگر تابع histeq : با در نظر گرفتن هیستوگرام هدف اگرهیستوگرام تصویر ورودی را اختصاصی به آن حرکت دهیم هیستوگرام یکنواخت میشود اگر به سمت هیستوگرام هدف حرکت دهیم با توجه به کاربرد آن تغییر شکل میدهد .

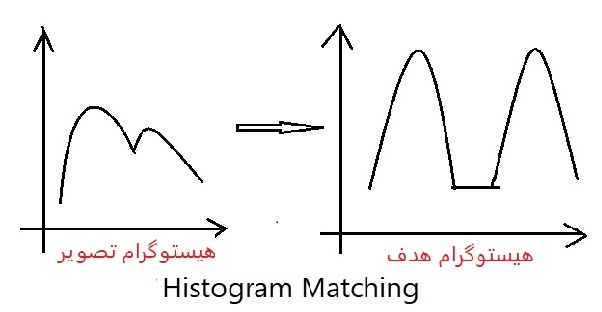
در تابع histeq وقتی که J = histeq  و I = hgram  باید هیستوگرام تصویر را طوری عوض کنید که حاصل هیستوگرام خروجی شود ، با اعداد صحیح تعداد روشنائی ها نشان داده میشود.

برای تصاویر دودویی تصویری با یونیت 8 درhgram برداری با 256 شاخصه باید داشته باشیم در تصاویر دابل تابع میدهیم به طور خودکار جمع شاخصه های هیستوگرام را برابر جمع نقاط خود تصویر قرار میدهد .  (hgram )

برای جمع اعداد هیستوگرامی باید اعداد هیستوگرام برابر تعداد کوچکترین نقاط تشکیل دهنده تصویر باشد (مجموع فراوانی همه داده ها  میشود مجموع کل فراوانی )

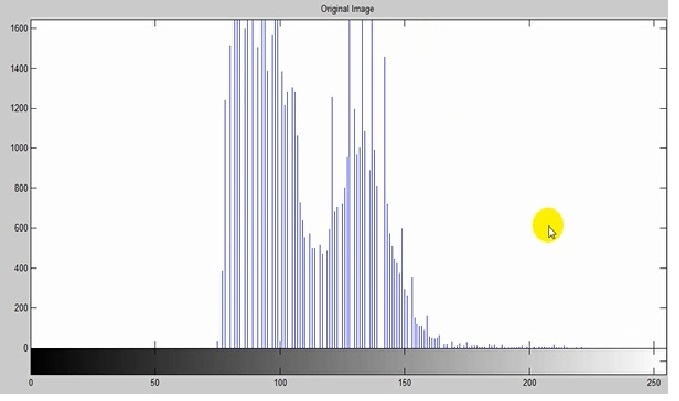
در هیستوگرام هدف شدت نور تصاویر متلب وتابع Hgram هیستوگرام خودکار محاسبه و نرمال میشود .

 

1. %% Load Image
   Mu = 180 ;
   Sigma = 30 ;
   H=@(X) exp(-1/(2*sigma^2)*(x-mu).^2;
   X=0:255;
   Hgram=H(x);
   stem(x,hgram);
   npixel=numel(img1);
   >>size(img1)
   Ans=
   291    240
   >>291*240
   Ans=
   69840
   >>prod(size))
   Ans=
   69840

  این گونه هم میتوانیم بنویسیم :

1. >>numel(img1)
   Ans =
   69840

کاری میکنیم مجموع Hgram  برابر npixel شود .

 

1. Hgram= Hgram/sum(hgram);
   >>sum(hgram)
   Ans=
   1.000
   >>hgram=npixel*hgram/sun(hgram);

با زدن F5 اعداد بزرگ و نمودار حاصل میشود .

 

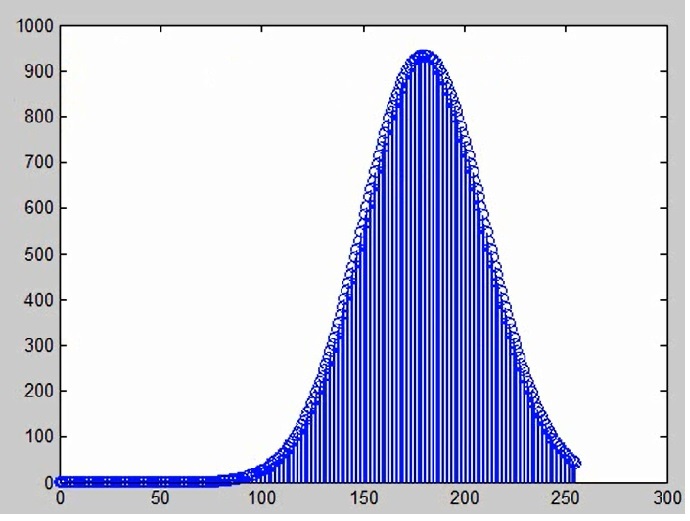
برای حساب کردن مجموع این ها :

 

1. >>sum(hgram)
   Ans=
   6.9840e+04

 پس به نزدیکترین عدد صحیح رُند میکنیم چون اعداد غیر صحیح هستند.

1. >>sum(hgram) Ans= 69832 
   >>npixel Npixel= 69840

در هیستوگرام هدف متلب و تابع Hgram  برای نشان دادن هیستوگرام به تصویر دیگر :

1. Img2=histeq(img1,hgram);
    % show Results
   Figure ;
   Subplot ( 2 , 2 , 1 ) ;
   imshow ( img 1 ) ;
   title ( ‘ original Image ‘ ) ;
   subplot ( 2 , 2 , 2 ) ;
   imshow ( img 2 ) ;
   title ( ‘ Result of histeq ‘ ) ;
   subplot ( 2 , 2 , 3 ) ;
   imhist ( img 1 ) ;
   subplot ( 2 , 2 , 4 ) ;
   imhist ( img 2 ) ;

تصویر پایین به دست آمد

 

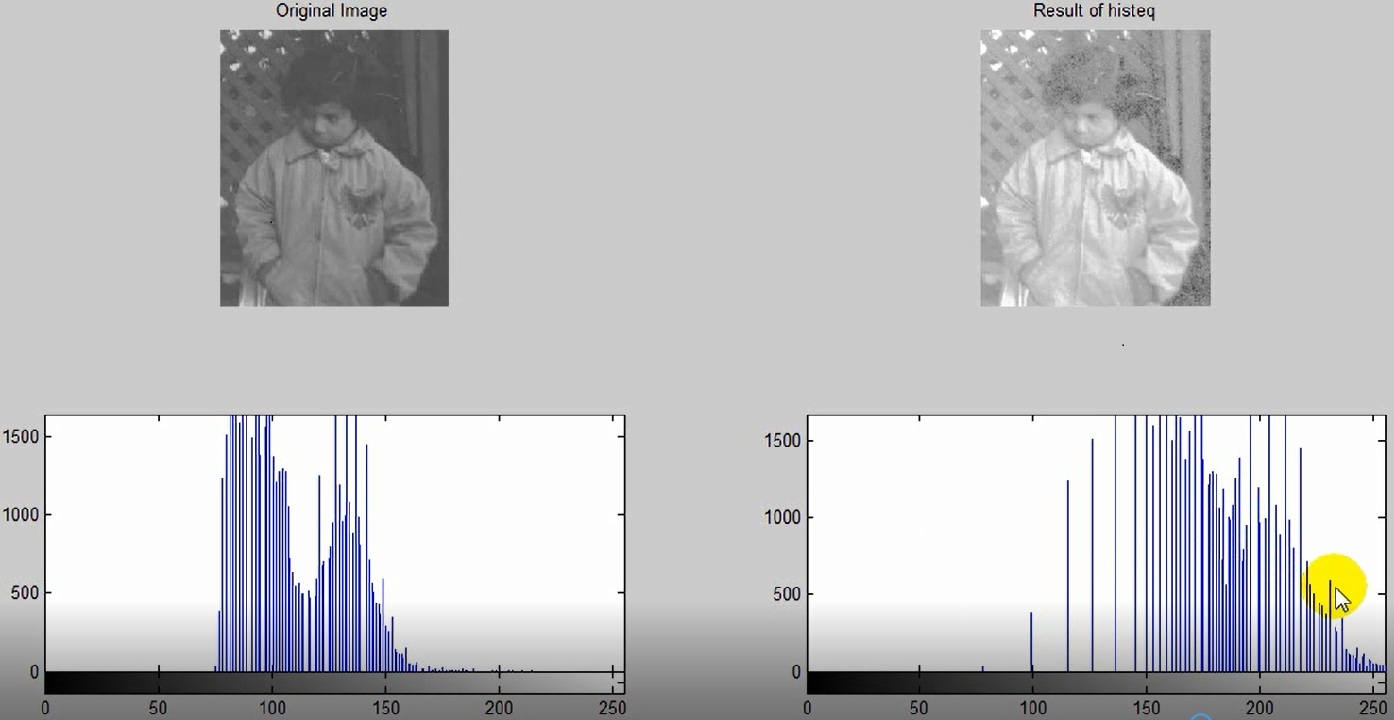
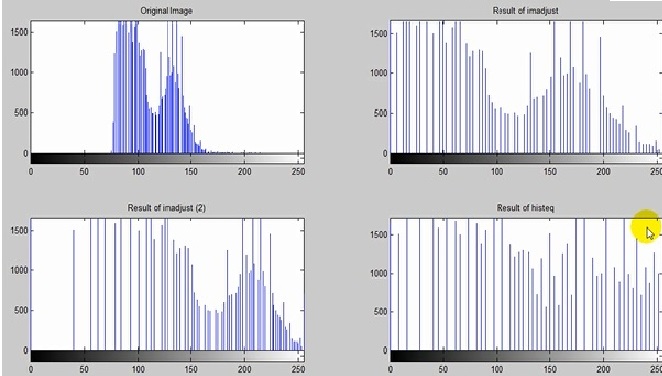
اگر بخواهیم نمودار دو قله ای  شود :

 

1. Img 1 imread ( ‘ pout . tif ‘ ) ;
   Npixel 1 = nume 1 ( img 1 ) ;
   W 1 = 5 ;
   Mu 1 = 50 ;
   Sigma 1 = 30 ;
   W2 = 10 ;
   Mu 2 =180 ;
   Sigma 2 = 50 ;
   H = @ ( X ) w 1 * exp ( -1 / ( 2 * sigma 1 ^ 2 ) * ( x – mu 1 ) . ^ 2 )  +w 2 * exp ( -1 / (2 * sigma 2 ^ 2 ) * (x – mu 2 ) . ^ 2 ) ;
   X = 0 : 255 ;
   Hgram = H ( x ) ;
   Hgram = round ( npixe 1 * hgram / sum ( hgram ) ) ;
   Img 2 = histeq ( img , hgram ) ;

 

 

 

 

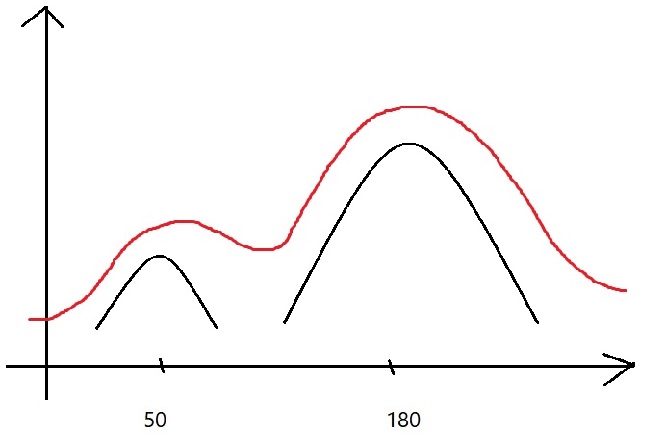
به این شکل میشود.

 

 با تغییراتی که بر هیستوگرام هدف شدت نور تصاویر متلب وتابع Hgram انجام میدهیم در جاهائی میتوانیم به شکل مطلوب برسیم .

چه طور میتوانیم به تفکیکی بهینه در بهترین هیستوگرام مبدا برسیم ؟

مثلا انحراف معیار را به شکل یک تابع هدف به میزان تفکیک پذیری در نظر میگیریم و به الگوریتم بهینه سازی میسپاریم تا در خروجی بین دو بخش از تصویر بیشترین تفکیک پذیری را داشته باشیم  (مثل الگوریتم کلاسیک یا الگوریتم ژنتیک )

در هیستوگرام مچینگ دو بار کار تبدیل انجام میشود یک بار تصویر را با هیستیکیو به تصویر با هیستوگرام یکنواخت تبدیل میکند و باز یکنواخت را به آن چیزی که ما میخواهیم تبدیل میکند .

برای هیستوگرام کوالیزیشن ابتدا رفتار تصادفی ابجکت ها در اشتراک گزاری با یک تابع توزیع احتمال را توصیف میکنیم .

نقطه ضعف این کار اینه که خط های تفکیک مشخص نیست در تابع adapthisteq با یک درون یابی خطی مرزها را عوض میکنیم وخطوط تفکیک مشخص میشود . ( با تقسیم بندی تصویر به بلوکها و جدا کردن کوالیزیشن هر بخش خطهای تفکیک مشخص میشوند )

 

1. %%Load Image
   Img1 = imread ( ‘pout . tif ‘ ) ;
   Img2 = adapthisteq (img 1) ;
   %% Show Results
   Figure ;
   Subplot ( 2 , 2 , 1 );
   Imshow (img 1) ;
   Title ( ‘ Original Image ‘) ;
   Subplot ( 2 , 2 , 2);
   Imshow (img2) ;
   Title ( ‘Result of adapthisteq ‘ );

 

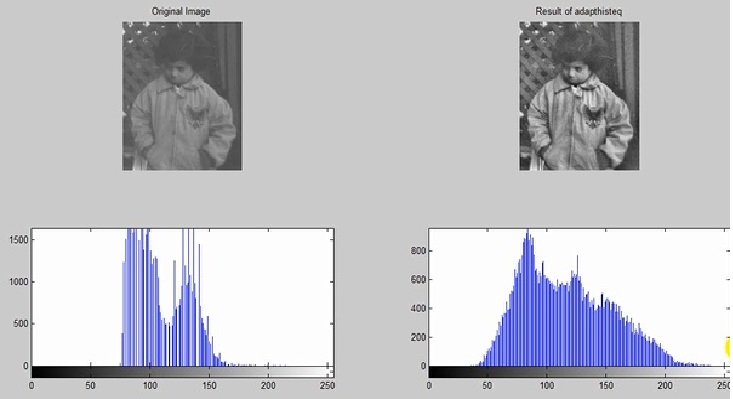
بیشتر مرکز گرا است بخش های مختلف را جداگانه آورده تا به این مکانیزم رسیده .

 بلوک های سازنده اپراتورهای خیلی بزرگتری هستند .

 ادامه آموزش متلب در بخش 8